Finding the energy cutoff and k-point is like the fundamental of doing DFT calculations. However there doesn't seem to be an universal way to do it. I found on the quantum-espresso forum
a very informative and thorough explanation. Thank Stefano for a such detailed post. Below is my notes on the procedures:
1. First test ecutwfc and ecutrho
Ecutwfc and ecutrho are properties related to the Fourier components that are needed to describe the wavefunctions and the density of the system. The convergence depends on the highest Fourier components. Each pseudopotential has a required cutoff: the upperbound. The cutoff needed for a system containing several species is the highest among those needed for each element.
- Increasing ecutwfc value while fixing ecutrho = 4*ecutwfc. Perform total energy (if possibly, force and stress) convergence tests until satisfactory stability is reached[1].
2. Fix the ecutrho from Step 1, and reduce ecutwfc. See how much ecutwfc can be reduced without deteriorating the convergence.
3. Fix ecutwfc from step 2 and ecutrho from step 1, identify appropriate k-point.
- This one is tricker because convergence with respect to k-points is a property of the band structure. There is a big difference between convergence in a band insulator and in a metal.
(I don't quite understand this part, but it seems like in an insulator, the k-point convergence is rather simple comparing to a metal. In an insulator, bands are completely occupied or empty across the Brillouin zone and charge density can be written in terms of wannier functions that are exponentially localized in real space. As a result, the convergence with respect to the density of point in the different directions in the Brillouin zone should be exponentially fast and quick. On the other hand, metals require much denser set of k points in order to locate accurately the Fermi surface. This induces that a smearing width smoothing the integral to be performed.... )
[1] Satisfactory stability is typically ~0.05 eV/atom for energy, and 10meV/A for forces. (Or ~1 mry/atom and 1.e04 ry/au in atomic units)
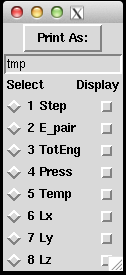 (About how to use Pizza.py, please refers to previous post of How to use Pizza.py for LAMMPS or the official Pizza.py Toolkit page.
Instead of asking pizza.py to get all the "Temp", "TotEng" .. by typing in each variable, and then do g.plot (a lot of repetitive keyboard work!), there's a much faster way to visualize the thermo-type data. It allows us to quickly view the trend of properties, and get an idea of the equilibrium status of the simulation.
This can be done directly on the shell or through pizza.py. Below is to do it in pizza.py:
(About how to use Pizza.py, please refers to previous post of How to use Pizza.py for LAMMPS or the official Pizza.py Toolkit page.
Instead of asking pizza.py to get all the "Temp", "TotEng" .. by typing in each variable, and then do g.plot (a lot of repetitive keyboard work!), there's a much faster way to visualize the thermo-type data. It allows us to quickly view the trend of properties, and get an idea of the equilibrium status of the simulation.
This can be done directly on the shell or through pizza.py. Below is to do it in pizza.py: